Die großen Fragen des Lebens – Woher kommen wir? Was ist Bewusstsein? Gibt es etwas nach dem Tod? – begegnen uns oft in spirituellen oder religiösen Kontexten. Gleichzeitig versuchen die Naturwissenschaften, die Welt möglichst präzise und messbar zu beschreiben. Viele Menschen empfinden dabei einen tiefen Graben zwischen Spiritualität und Wissenschaft, als wären sie zwei unvereinbare Sprachen.

Mit meiner Philosophie des Evolutionären Idealismus (EvId) versuche ich, genau diese Trennung zu überwinden. Nicht oberflächlich, nicht als bloßes „Brückenbauen“, sondern als wirklich integrative Theorie, die beide Perspektiven – die innere Erfahrung des Bewusstseins und die äußere Beschreibung der Welt – auf ein gemeinsames Fundament stellt: Information.

Im Zentrum dieser Philosophie steht ein Konzept, das ich Info-Spin nenne. Es geht davon aus, dass Raum und Zeit nicht objektiv „da draußen“ existieren, sondern Interpretationen einer tieferliegenden Informationsmatrix sind – hervorgebracht durch das Bewusstsein. Und: Vor der Geburt und nach dem Tod tauschen Raum und Zeit ihre Rollen. Diese Idee wirkt auf den ersten Blick abstrakt oder sogar esoterisch, gerade weil sie sich nicht an Alltagslogik orientiert. Und doch lässt sich zeigen, dass diese Sichtweise nicht nur philosophisch, sondern auch physikalisch plausibel sein kann.

Um genau das zu demonstrieren, habe ich einen wissenschaftlichen Fachartikel geschrieben:
„The Event Horizon as Origin: A Perspective-Based Interpretation of Black Hole Spacetime“.

Darin zeige ich, dass es einen Ort im Universum gibt, an dem sich tatsächlich beobachten lässt, wie Raum und Zeit ihre Funktionen vertauschen – den Ereignishorizont eines Schwarzen Lochs. Diese Perspektive könnte helfen, einige ungelöste Rätsel der Physik zu klären: etwa, warum die theoretisch vorhergesagten weißen Löcher nie beobachtet wurden, wie man sich den Urknall jenseits einer Singularität vorstellen kann, und wie das Verhältnis zwischen Beobachter und Raumzeit neu gedacht werden muss.

Noch läuft das Peer-Review-Verfahren, das über die wissenschaftliche Veröffentlichung entscheidet. Doch ich möchte meine Gedanken schon jetzt mit einem breiteren Publikum teilen – auch mit Menschen, die sich nicht täglich mit Relativitätstheorie oder Quantenphysik beschäftigen. Denn die Fragen, die sich an den Rändern unseres Wissens auftun, betreffen uns alle: Wer sind wir, wenn die Kategorien von Raum und Zeit selbst relativ werden? Man kann den Artikel lesen, ohne die mathematischen Formeln zu beachten, dann bekommt man einen Eindruck, worum es dabei geht. Ich werde in einem der Folgeartikel aber auch noch versuchen, die Grundaussage in Verbindung mit dem Evolutionären Idealismus in leicht verständlicher Sprache darzustellen. Für alle, die darauf nicht warten wollen, ist hier der Fachartikel (auch als PDF-Download verfügbar) in der deutschen Übersetzung:

—————————————————————————–

Der Ereignishorizont als Ursprung: Eine perspektivische
Interpretation der Raumzeit von Schwarzen Löchern

Abstract

In diesem Beitrag wird eine alternative Interpretation des Ereignishorizonts Schwarzer Löcher vorgeschlagen, die auf einer Analyse der Raumzeitstruktur im Inneren des Horizonts beruht. Während die klassische Außensicht auf Schwarze Löcher von einem radialen Kollaps geprägt ist, zeigt eine koordinatentransformierte Binnenperspektive, dass sich die Rollen von Raum und Zeit vertauschen: Der Raum wird eindimensional und zeitartig, während die ehemalige Zeitkoordinate eine neue raumartige Struktur annimmt. Diese Perspektive legt nahe, dass der Ereignishorizont intern als Urknall erscheinen könnte – als ein Punkt, von dem alles zeitlich divergiert. Auf dieser Grundlage wird die Hypothese entwickelt, dass das Phänomen des Weißen Lochs in einem solchen Modell nicht als gesondertes Objekt, sondern als kosmologischer Ursprung (Urknall) zu deuten ist. Der Artikel skizziert eine mathematische Darstellung dieser Perspektivumkehr auf Basis der Schwarzschild-Metrik und diskutiert die konzeptuellen Implikationen für die kosmologische Modellbildung. Abschließend werden mögliche experimentelle und theoretische Ansätze zur Überprüfung der Hypothese vorgestellt. Die Überlegung versteht sich als Beitrag zu einer relationalen Auffassung von Raum und Zeit in gravitativen Extrembereichen.

1. Einleitung

Die allgemeine Relativitätstheorie beschreibt Schwarze Löcher als Regionen extremer Raumzeitkrümmung, in denen die Fluchtgeschwindigkeit am Ereignishorizont der Lichtgeschwindigkeit entspricht. Jenseits dieses Horizonts kollabiert die Raumzeit unumkehrbar in Richtung einer zentralen Singularität – so die etablierte Außensicht. Doch was geschieht innerhalb des Ereignishorizonts? Ist es möglich, eine alternative, innere Perspektive zu entwickeln, die nicht nur mathematisch konsistent, sondern auch konzeptionell aufschlussreich ist?

Dieser Artikel geht der Hypothese nach, dass sich aus der Binnenperspektive eines Schwarzen Lochs die Struktur der Raumzeit fundamental verändert: Die zeitliche und die radiale (räumliche) Koordinate tauschen ihre Rollen, sodass die Bewegung in Richtung der Singularität nicht mehr als räumliches Fallen, sondern als unausweichlicher zeitlicher Verlauf interpretiert werden kann. Diese Betrachtungsweise führt zu einer überraschenden Analogie: Aus Sicht eines hypothetischen Beobachters im Inneren erscheint der Ereignishorizont nicht als Grenze, sondern als Ursprung – analog zu einem Urknall, von dem sich alles entfernt.

Im Folgenden wird diese Hypothese zunächst auf Grundlage der Schwarzschild-Metrik mathematisch entwickelt. Anschließend diskutieren wir ihre Konsequenzen für unser Verständnis kosmologischer Anfangszustände, insbesondere im Hinblick auf die bislang hypothetische Existenz Weißer Löcher. Der Artikel schließt mit einem Ausblick auf mögliche Wege zur empirischen oder theoretischen Prüfung der These sowie mit philosophischen Überlegungen zur Relativität von Raum, Zeit und Perspektive in gravitativen Grenzbereichen.

2. Physikalische Grundlage: Raumzeitstruktur Schwarzer Löcher

Schwarze Löcher sind Lösungen der Einstein-Gleichungen, in denen die Raumzeit derart gekrümmt ist, dass innerhalb eines bestimmten Radius – des Ereignishorizonts – kein Signal mehr nach außen gelangen kann. Die einfachste und am häufigsten untersuchte Lösung ist die Schwarzschild-Metrik, die das Gravitationsfeld eines nicht rotierenden, ungeladenen Massepunkts beschreibt. In natürlichen Einheiten (c = G = 1) lautet sie:

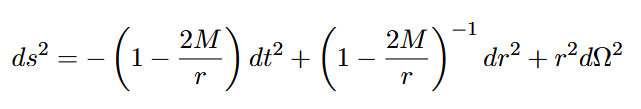
mit

• ds²: Linienelement der Raumzeit
• t: Zeitkoordinate
• r: radialer Abstand zur Singularität
• M : Masse des Schwarzen Lochs
• dΩ² = dθ² + sin² θ dϕ²: Winkelanteil der Metrik

Am Ereignishorizont bei r = r_s = 2M wird der Term (1 – (2M/r)) null, was zu einer Koordinatensingularität führt: Das Vorzeichen des Metriktensors kehrt sich um. Dies deutet bereits darauf hin, dass sich dort grundlegende Eigenschaften der Raumzeit ändern.

2.1. Der Koordinatentausch: Zeit wird Raum – Raum wird Zeit

Innerhalb des Ereignishorizonts (r < 2M ) wird der Faktor vor dt² positiv, während jener vor dr² negativ wird. Das bedeutet:

• t wird zu einer raumartigen Koordinate
• r wird zu einer zeitartigen Koordinate

Diese Umkehr ist mehr als ein mathematischer Trick – sie hat tiefgreifende konzeptionelle Implikationen: Das, was wir außerhalb des Ereignishorizonts als ”räumliches Fallen” in Richtung Zentrum deuten, entspricht innerhalb einer unausweichlichen Entwicklung in der Zeit. Für einen freien Fallenden gibt es kein Verharren bei konstantem r; das Fortschreiten in Richtung der Singularität ist notwendig – wie das Fortschreiten in der Zeit in unserer Alltagswelt.

2.2. Interpretation des Raumzeitverlaufs

Ein Beobachter im freien Fall erlebt dieses Geschehen jedoch als regular: Die Eigenzeit verläuft kontinuierlich, ohne spürbare Diskontinuität beim Passieren des Ereignishorizonts. Aus seiner Sicht ist der Horizont kein physikalisch markanter Ort – die Singularität hingegen ist unausweichlich. Dies erlaubt eine Umdeutung:

• Von außen erscheint der Horizont als Raumgrenze
• Von innen jedoch könnte er als zeitlicher Ursprung erscheinen

An dieser Stelle setzt die zentrale These dieses Artikels an: Wenn sich innerhalb des Ereignishorizonts die Zeit in den Raum hinein entfaltet und der Raum kollabiert, dann entspricht dies formal genau der umgekehrten Dynamik eines expandierenden Universums – wie wir sie aus der Kosmologie kennen.

2.3. Parallele zur kosmologischen Metrik

Zum Vergleich: Die Friedmann-Lemaitre-Robertson-Walker-Metrik eines expandierenden Universums lautet:

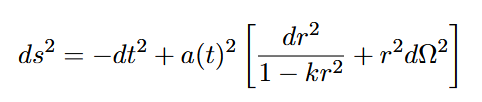
Hier ist t eine echte Zeitkoordinate, und der Skalenfaktor a(t) beschreibt die Expansion des Raumes. Vergleicht man dies mit dem inneren Teil der Schwarzschild-Metrik (bei r<2M), so zeigt sich formal eine ähnliche Struktur – jedoch mit vertauschten Rollen von Raum und Zeit.

Diese Beobachtung eröffnet die Möglichkeit, den Raumzeitverlauf innerhalb eines Schwarzen Lochs als invertierte kosmologische Expansion zu interpretieren – nicht als Kollaps, sondern als zeitliche Divergenz von einem gemeinsamen Ursprung, dem Ereignishorizont.

3. Mathematische Formulierung: Der Ereignishorizont als Ursprung in vertauschter Raumzeitstruktur

Um die Struktur der Raumzeit innerhalb des Ereignishorizonts physikalisch und geometrisch greifbar zu machen, ist es hilfreich, von der Schwarzschild-Metrik in koordinatenreguläre Darstellungen zu wechseln. Eine besonders geeignete Wahl sind die Kruskal-Szekeres-Koordinaten, die die scheinbare Singularität bei r=2M auflösen und eine globale Betrachtung der Raumzeit ermöglichen.

3.1. Von Schwarzschild zu Kruskal-Szekeres

Ausgehend von der Schwarzschild-Metrik:

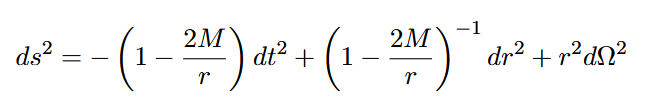
Die Schwarzschild-Metrik besitzt bei r=2M eine Koordinatensingularität, keine physikalische. Um die Raumzeitstruktur vollständig zu beschreiben, definieren wir neue Koordinaten (U,V), in denen sich die Metrik regulär schreiben lässt.

Zunächst führen wir die sogenannten „Tortoise-Koordinaten“ r_* ein:

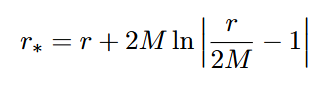
Dies ermöglicht die Einführung von Nullkoordinaten:

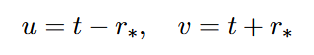
die dann zur Definition der Kruskal-Szekeres-Koordinaten verwendet werden:

Damit ergibt sich die Metrik in Kruskal-Szekeres-Koordinaten als:

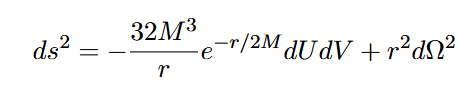
Hier ist r implizit durch die Beziehung zwischen U, V und r_* definiert.

3.2. Bedeutung der Kruskal-Darstellung

Diese Darstellung hat mehrere entscheidende Vorteile:

• Die Metrik ist glatt ¨uber den Horizont hinweg, insbesondere bei r = 2M
• Die kausale Struktur ist explizit sichtbar
• Die Zeitpfeile in verschiedenen Bereichen der Raumzeit können analysiert werden

In der Kruskal-Darstellung wird deutlich, dass sich die Struktur der Raumzeit in vier Regionen gliedert:

1. Außenregion (Region I) – wie die bekannte Außenwelt
2. Innenregion (Region II) – innerhalb des Ereignishorizonts
3. Weiße-Loch-Region (Region III) – Spiegelbild des Schwarzen Lochs
4. Paralleluniversum (Region IV) – rein mathematisches Artefakt ohne physikalische Entsprechung

Für unsere These ist Region II entscheidend. Dort zeigt sich, dass die Koordinate r, ursprünglich eine Raumkoordinate, zu einer zeitartigen Richtung wird – und jeder Kausalverlauf notwendigerweise in Richtung kleinerer r verläuft, bis zur Singularität r=0. Dies ist keine Option, sondern eine Notwendigkeit: Wie im Universum niemand „zum Urknall zurückkehren“ kann, kann auch niemand innerhalb des Schwarzen Lochs zum Ereignishorizont zurückkehren.

3.3. Perspektivumkehr: Horizont als Anfang

Nun erfolgt der zentrale interpretative Schritt:

• In der üblichen (externen) Sicht ist der Ereignishorizont die Grenze eines kollabierenden räumlichen Objekts.
• In der internen (koordinatentransformierten) Sicht jedoch entspricht er einem zeitlichen Anfangspunkt – alle Kausalverläufe divergieren davon weg

Formal ergibt sich ein symmetrisches Diagramm zur kosmologischen Raumzeitentwicklung:
Der Ereignishorizont spielt dieselbe Rolle wie die t=0-Hypersurface im Standardmodell der Kosmologie.

Diese Struktur legt nahe, dass der Ereignishorizont aus interner Sicht wie ein Urknall wirkt – als Ursprung einer Zeitrichtung, in deren Verlauf sich alle Zustände in Richtung einer finalen Singularität entwickeln. Dieser „invertierte Kosmos“ ist jedoch aus externer Sicht vollständig kollabiert.

3.4. Kausalstruktur und Informationsfluss

Ein bemerkenswerter Aspekt ist, dass diese Struktur auch Aufschluss über die thermodynamischen Asymmetrien gibt:

• In der äußeren Welt ist der Ereignishorizont eine Einweg-Grenze für Information (Information kann hinein-, aber nicht herausgelangen).
• In der inneren Welt ist er der Beginn aller Kausalverläufe, ähnlich wie der Urknall, von dem keine Information stammt, aber alle ausgeht

Dies legt eine tiefe strukturelle Analogie nahe, nicht nur formal, sondern auch hinsichtlich des Informations- und Energieverhaltens.

4. Weiße Löcher und der Urknall: Zwei Namen für ein Phänomen?

In der klassischen Lösung der allgemeinen Relativitätstheorie – insbesondere in der maximal fortgesetzten Schwarzschild-Metrik – treten nicht nur Schwarze Löcher (Region II), sondern auch sogenannte Weiße Löcher (Region III) auf. Diese gelten als zeitliche Spiegelbilder Schwarzer Löcher:
Ein Weißes Loch ist ein Bereich der Raumzeit, aus dem nichts eindringen kann, aus dem jedoch Materie und Information herausströmen, ohne eine physikalische Ursache innerhalb der Raumzeitstruktur.

Während Schwarze Löcher inzwischen durch vielfältige astronomische Beobachtungen bestätigt sind (z.B. Gravitationswellen, Akkretionsscheiben, Schattenbilder), gibt es keinerlei empirische Hinweise auf die Existenz Weißer Löcher. Diese asymmetrische Beobachtungslage stellt die theoretische Symmetrie in Frage – und bietet einen Anknüpfungspunkt für unsere These.

4.1. Der Urknall als Weißes Loch?

Die Perspektivumkehr innerhalb des Schwarzen Lochs führt zu einer erstaunlichen Analogie:
Wenn sich der Ereignishorizont von innen wie ein Anfangspunkt darstellt, von dem alle Ereignisse zeitlich wegstreben, dann ist seine Struktur funktional identisch mit der kosmologischen Initialbedingung – dem Urknall.

Der Unterschied besteht dabei nicht in der lokalen Struktur, sondern im globalen Kontext:

• In einem Schwarzen Loch endet der ”interne Kosmos“ in einer zentralen Singularität
• Im kosmologischen Modell beginnt der beobachtbare Kosmos aus einer Singularität heraus

In beiden Fällen sind diese Singularitäten allerdings keine physikalisch beobachtbaren Punkte, sondern Grenzen der klassischen Theorie. Die strukturelle Analogie legt nun nahe, dass Weiße Löcher nicht als separate Objekte auftreten müssen – weil das Universum selbst als deren physikalische Realisierung gedeutet werden kann.
Diese Hypothese hat weitreichende Implikationen:

• Der Urknall ist kein externer Anfangspunkt, sondern die innere Perspektive auf einen kosmologischen Horizont
• Weiße Löcher existieren nicht zusätzlich, weil sie identisch mit dem Anfang unseres Kosmos sind
• Das Schwarzschild-Schwarze-Loch-Modell liefert eine lokale Kopie des kosmischen Anfangsprozesses – allerdings mit umgekehrtem Zeitpfeil und finaler statt initialer Singularität

4.2. Thermodynamische und kausale Aspekte

Ein zentraler Einwand gegen Weiße Löcher in der klassischen Theorie ist ihre thermodynamische Unplausibilität:
Sie würden „aus dem Nichts“ geordnete Energie und Information ausstoßen – eine Umkehr der Entropierichtung, die unserem Erfahrungsuniversum widerspricht.
Die Identifikation des Urknalls mit einem kosmischen Weißen Loch entschärft dieses Problem:

• Die Entropie war beim Urknall minimal, wächst seitdem – in Übereinstimmung mit der zweiten Hauptsatz
• Der kausale Horizont des Urknalls ist ebenso ein Einweg-Horizont, jedoch in umgekehrter Richtung wie beim Schwarzen Loch

Somit ist die thermodynamische Asymmetrie zwischen Schwarzen und Weißen Löchern keine Unstimmigkeit der Theorie, sondern ein Reflex der Perspektive – abhängig davon, ob der Beobachter außerhalb oder innerhalb des Horizonts verortet ist.

4.3. Ein Universum in jedem Schwarzen Loch?

Ein spekulativer, aber folgerichtiger Gedanke schließt sich an:
Wenn ein Ereignishorizont aus Binnenperspektive wie ein Urknall erscheint – könnte jedes Schwarze Loch der „Keim“ eines neuen Universums sein?

Diese Idee wurde bereits in unterschiedlichen Kontexten diskutiert – etwa in Lee Smolins Theorie der kosmologischen natürlichen Selektion oder in Modellen der Loop-Quantengravitation, in denen der Kollaps in eine neue expandierende Raumzeit übergeht (→ Bounce-Modelle).

Unsere Darstellung liefert eine geometrisch-kausale Grundlage für diese These, indem sie zeigt, dass bereits in der klassischen Relativitätstheorie eine solche Deutung formal zulässig ist – ohne zusätzliche Postulate. Der entscheidende Schritt ist die Akzeptanz, dass Perspektiven innerhalb und außerhalb eines Horizonts komplementäre Sichtweisen derselben Raumzeitstruktur sein können.

5. Implikationen und Überprüfbarkeit der Hypothese

Die vorgeschlagene Perspektivumkehr im Inneren eines Schwarzen Lochs – bei der der Ereignishorizont als kosmologischer Anfangspunkt erscheint – eröffnet neue Deutungsmöglichkeiten für die Struktur von Raum und Zeit im gravitativen Extrembereich. Zugleich stellt sich die Frage: Ist diese Hypothese rein spekulativ oder auf irgendeine Weise prüfbar?

In diesem Abschnitt sollen drei mögliche Zugänge skizziert werden:

1. theoretisch-mathematisch,
2. beobachtungsbasiert,
3. experimentell-analogisch.

5.1. Theoretische Ansätze: Modellvergleich und Kompatibilität

Eine erste Form der Überprüfung besteht im \textbf{Vergleich der Hypothese mit bestehenden Modellen} der Gravitationstheorie, insbesondere jenseits der klassischen Relativitätstheorie:

• Loop-Quantengravitation: In bestimmten Modellen ergibt sich beim Kollaps eines Schwarzen Lochs ein quantenmechanischer Bounce, der eine neue expandierende Raumzeit entstehen lässt. Die hier vertretene These könnte als klassische Grenzform solcher Modelle gedeutet werden – eine Art „semi-klassisches“ Korrelat der quanteninduzierten Re-Expansion.
• Einstein-Cartan-Theorie: In dieser Erweiterung der allgemeinen Relativitätstheorie verhindert der Torsionsterm eine Singularität und ersetzt sie durch einen Zustand maximaler Dichte – auch hier könnten invertierte Kausalstrukturen auftreten.
• Zyklische Kosmologien und Multiversum-Szenarien: In der Hypothese, dass jedes Schwarze Loch den Anfang eines neuen Kosmos markiert, findet sich eine formale Affinität zu bestimmten Varianten des kosmologischen „Evolutionsprinzips“ (Smolin) oder zum branching multiverse

Ein systematischer Vergleich der raumzeitlichen Kausalstrukturen in diesen Modellen mit den Koordinatenverläufen innerhalb klassischer Metriken könnte ein erster Schritt zu einer fundierteren Analyse sein.

5.2. Beobachtbare Signaturen?

Die direkte Beobachtung des Inneren eines Schwarzen Lochs ist prinzipiell unmöglich – doch es gibt indirekte Hinweise, die mit der Hypothese in Beziehung gesetzt werden könnten:

• Hawking-Strahlung: Diese quantenphysikalische Emission lässt vermuten, dass Schwarze Löcher nicht vollkommen informationsdichte Objekte sind. Wenn sie einen inneren kausalen Ursprung besitzen, könnte dies Einfluss auf das thermodynamische Verhalten der Strahlung haben. Modelle, die dies simulieren, könnten Unterschiede aufweisen zwischen rein kollapsbasierten und „geburtsartigen“ Interpretationen.
• Gravitationswellenanalyse: Extrem präzise Beobachtungen von Verschmelzungen Schwarzer Löcher könnten, zumindest theoretisch, Hinweise auf subtile Differenzen in der internen Struktur liefern – insbesondere in der Phase kurz vor dem Erreichen des gemeinsamen Horizonts.
• Kosmologische Hintergrundstrahlung: Wenn unser gesamter Kosmos die innere Dynamik eines kosmischen Ereignishorizonts ist, könnten sich in der großräumigen Struktur des Universums – etwa in Anisotropien der Hintergrundstrahlung – Hinweise auf eine solche kausale Herkunft finden lassen.

Zugegeben: All diese Hinweise sind spekulativ und indirekt. Aber sie können als heuristische Ankerpunkte dienen, um gezielt in Daten und Modellen nach Anomalien zu suchen, die mit der These kompatibel wären.

5.3. Analoge Modelle in Laborumgebungen

Bestimmte Laborsysteme wurden zur Simulation von Aspekten der Physik Schwarzer Löcher verwendet:

• Bose-Einstein-Kondensate
• Oberflächenwellen in Flüssigkeiten
• Nichtlineare optische Medien

Ein bemerkenswerter Befund ist, dass in bestimmten Konfigurationen auch Hawking-artige Strahlung nachgewiesen werden konnte – ein Hinweis darauf, dass selbst in nicht-gravitativen Kontexten Horizonte entstehen können, die mit unserer Theorie vergleichbar sind.

Die Frage ist:
Könnte man ein solches Analogmodell so konfigurieren, dass es eine Perspektivumkehr im Inneren eines „Horizonts“ erlaubt? Beispielsweise:

• ein zeitlich invertierter Kegel innerhalb eines Medienflusses
• eine gerichtete Informationsstruktur, bei der die Richtung der Kausalität ab einem Punkt fixiert ist
• oder eine rekonstruktive Simulation der Koordinatenumkehr aus der Kruskal-Szekeres-Transformation

Derartige Experimente könnten helfen, die Kausalstruktur visuell und konzeptionell zugänglich zu machen – auch wenn sie keine Beweise im strengen Sinne liefern können.

5.4. Philosophische Implikationen: Perspektivität als Raumzeitprinzip

Ein metatheoretischer Gewinn der hier entwickelten These liegt in ihrer Betonung der Beobachterperspektive. Sie macht deutlich:

• Die Struktur der Raumzeit ist nicht absolut, sondern kontextabhängig, insbesondere in Bereichen extremer Gravitation.
• Begriffe wie „Anfang“, „Ende“, „Raum“ und „Zeit“ verlieren im Inneren eines Schwarzen Lochs ihre klassische Bedeutung und werden \textbf{relational}.
• Das Universum könnte – in gewissem Sinne – aus sich selbst heraus entstehen, wenn Raumzeitbereiche durch Horizonte kausal entkoppelt und rekursiv organisiert sind.

Diese Sichtweise verbindet die moderne Relativitätstheorie mit alten philosophischen Fragen nach dem Ursprung von Raum und Zeit – und stellt sie in einen dynamischen, beobachterrelativen Rahmen.
Dies unterstützt ein relationales und perspektivisches Verständnis der Kosmologie, das sich in den Rahmen meiner philosophischen Theorie des „Evolutionären Idealismus“ einfügt.

6. Fazit und Ausblick: Die Relativität des Ursprungs

In diesem Beitrag wurde die Hypothese untersucht, dass der Ereignishorizont eines Schwarzen Lochs aus einer geeigneten Binnenperspektive nicht als Grenze, sondern als Ursprung erscheint – als ein Punkt, von dem alle Kausalverläufe zeitlich wegstreben. Diese Perspektive ergibt sich aus einer Analyse der Raumzeitstruktur in der Schwarzschild-Metrik, insbesondere nach dem Durchgang durch den Ereignishorizont, bei dem sich Raum- und Zeitkoordinaten in ihrer Funktion vertauschen.

Durch diese Perspektivumkehr zeigt sich der Horizont formal und strukturell analog zum kosmologischen Urknall. Damit bietet sich eine Erklärung an, warum Schwarze Löcher beobachtbar sind, Weiße Löcher jedoch nicht: Sie sind nicht zwei getrennte Objekte, sondern zwei Betrachtungsweisen ein und desselben Phänomens – je nachdem, ob man sich außerhalb oder innerhalb eines kausal geschlossenen Raumzeitbereichs befindet.

Diese These hat weitreichende Implikationen:

• Sie liefert eine neue Interpretation der Raumzeitstruktur im gravitativen Extrembereich, die klassische und kosmologische Perspektiven miteinander verbindet.
• Sie stärkt die Position relationaler Raumzeittheorien, in denen Beobachterstandpunkte konstitutiv für physikalische Aussagen sind.
• Sie eröffnet Möglichkeiten für die heuristische Modellierung von „Universen in Schwarzen Löchern“, ohne auf spekulative Quantengravitationsannahmen zurückgreifen zu müssen.

Zugleich bleibt der Zugang zur empirischen Überprüfung begrenzt – was angesichts des prinzipiell kausal abgeschirmten Inneren Schwarzer Löcher nicht überrascht. Doch gerade deshalb könnten neue Wege beschritten werden: über vergleichende Modellanalysen, Simulationen in analogen Systemen oder durch philosophisch fundierte Reinterpretationen bestehender Theoriemodelle.

Ausblick: Fragen für die weitere Forschung

• Lässt sich ein formales Kriterium dafür aufstellen, wann ein Horizont als zeitlicher Anfang und nicht als räumliche Grenze erlebt wird?
• Wie verhält sich der Entropiefluss bei solchen Perspektivenwechseln – und was bedeutet das für den zweiten Hauptsatz der Thermodynamik?
• Könnten künftige Entwicklungen in den Theorien der Quantengravitation (z. B. Kausalmengen-Theorie, emergente Raumzeit) diese Hypothese unterstützen oder verfeinern?
• Und vielleicht am faszinierendsten: Könnte das Universum rekursiv sein – fähig, aus sich selbst heraus immer wieder neue kausale Bereiche zu erzeugen?

Diese und ähnliche Fragen verweisen auf die Tiefe und das offene Potenzial des hier skizzierten Denkansatzes – als physikalische Spekulation, als theoretische Methode und als philosophische Reflexion über die Grenzen unserer Raumzeitvorstellungen.
Dies unterstützt ein relationales und perspektivisches Verständnis der Kosmologie, das sich in den Rahmen meines Evolutionären Idealismus einfügt.

Anhang A: Mathematische und geometrische Ergänzungen

A.1 Herleitung der Kruskal-Szekeres-Koordinaten

Ausgangspunkt ist die Schwarzschild-Metrik:

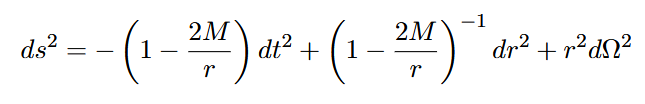
Zur Vermeidung der Koordinatensingularität bei r=2M wird zunächst die „Tortoise-Koordinate“ r_* eingeführt:

Daraus konstruieren wir die Nullkoordinaten:

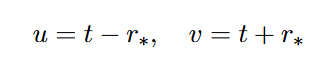
und definieren die Kruskal-Szekeres-Koordinaten wie folgt:

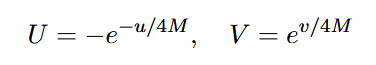
In diesen Koordinaten ergibt sich die Schwarzschild-Metrik:

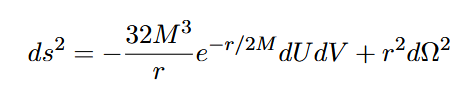
A.2 Kausalstruktur und Raumzeitregionen

Die Kruskal-Koordinaten decken vier Bereiche ab:

I – Außenwelt (Schwarzes Loch) – r>2M
II – Inneres des Schwarzen Lochs – r>2M, r zeitartig
III – „Weißes Loch“-Region – r>2M, Vergangenheit der Außenwelt
IV – Paralleles Universum (nicht verbunden) – rein mathematisch

A.3 Penrose-Diagramm

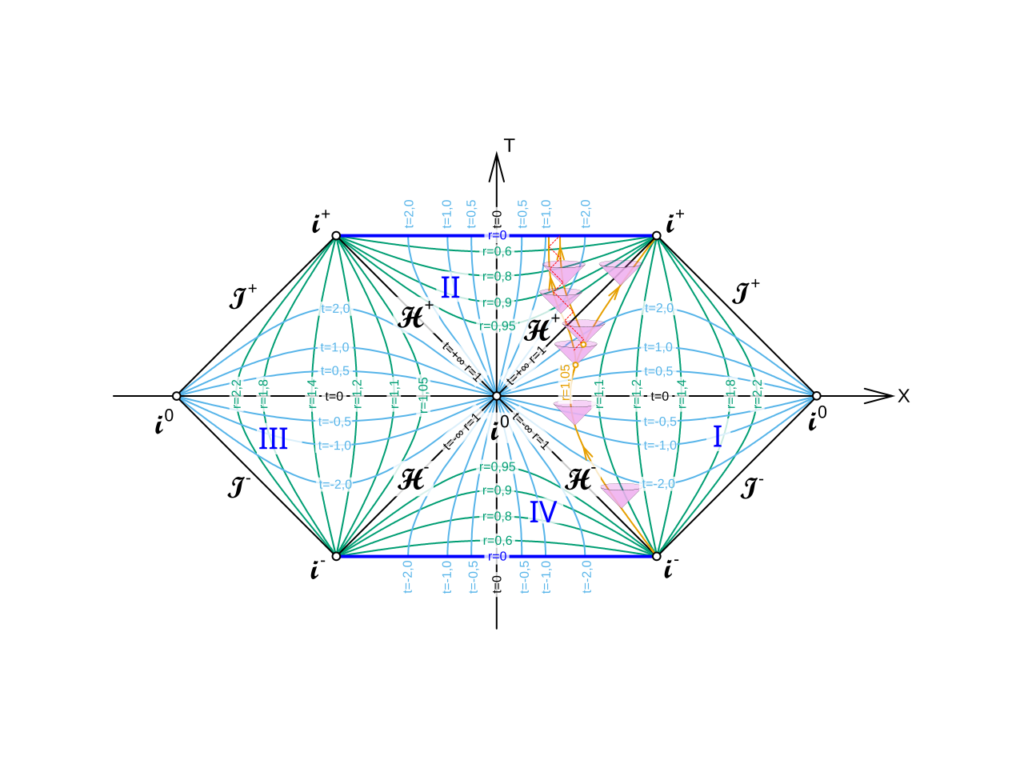
Abbildung: Penrose-Diagramm der Schwarzschild-Raumzeit mit vier kausal unterschiedlichen Regionen.

A.4 Vergleich mit FLRW-Metrik

Zum Vergleich die FLRW-Metrik:

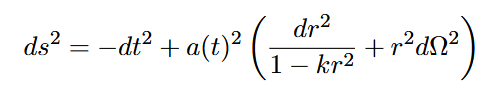
Hier ist t die kosmische Zeit, a(t) der Skalenfaktor. Im Unterschied zur Schwarzschild-Metrik ist hier der „Raum“ expandierend, die „Zeit“ universal. Die in Abschnitt 3 dargestellte Perspektivumkehr macht deutlich, dass der Ereignishorizont in der Schwarzschild-Metrik formal dieselbe kausale Rolle spielt wie t=0 in der FLRW-Metrik – jedoch lokal statt global.

Referenzen

S. W. Hawking, “Particle creation by black holes,” Communications in Mathematical Physics, 43.3 (1975): 199–220.
M. D. Kruskal, “Maximal extension of Schwarzschild metric,” Physical Review, 119.5 (1960): 1743–1745.
K. S. Thorne, Black Holes and Time Warps: Einstein’s Outrageous Legacy, W. W. Norton & Company, 1994.
A. Ashtekar, M. Bojowald, “Black hole evaporation: A paradigm,” Classical and Quantum Gravity, 22 (2005): 3349–3362.
L. Smolin, The Life of the Cosmos, Oxford University Press, 1997.
C. Rovelli, F. Vidotto, “Planck stars,” International Journal of Modern Physics D, 23.12 (2014): 1442026.

Autorenhinweis

Gerhard Höberth ist ein unabhängiger Philosoph mit Sitz in Süddeutschland. Seine Arbeit verbindet Physik, Metaphysik und Systemtheorie und konzentriert sich auf die Entwicklung der Philosophie des Evolutionären Idealismus – ein Rahmenwerk, das versucht, wissenschaftliche Kosmologie mit spiritueller Tiefe im Dienste eines integralen Verständnisses von Realität und Transformation zu integrieren.